THỂ TÍCH HÌNH CHÓP

Hình học không gian là phần rất quan trọng trong toán hình học mà các em học sinh cần nẵm vững. Tính thể tích hình chóp cũng là 1 dạng toán hình hoc không gian có nhiều dạng bài tập khác nhau. Mời các em cùng tìm hiểu về thể tích của hình chóp và các dạng toán thường gắp qua bài viết dưới đây.

ĐỊNH NGHĨA HÌNH CHÓP

Hình chóp là một hình không gian gồm có một đa giác gọi là mặt đáy, các tam giác chung đỉnh gọi là mặt bên, đỉnh chung của các mặt bên đó gọi là đỉnh của hình chóp (h.2.4)

[caption id="attachment_2913" align="aligncenter" width="232"]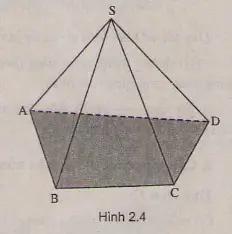 Hình chóp[/caption]

CÔNG THỨC TÍNH THỂ TÍCH HÌNH CHÓP

Gọi A_d là diện tích đáy, h là chiều cao của khối chóp (khoảng cách từ đỉnh đến mặt đáy), V là thể tích hình chóp. Ta có công thức tính thể tích hình chóp như sau

V=(A_d.h)/3

[caption id="attachment_2914" align="aligncenter" width="240"]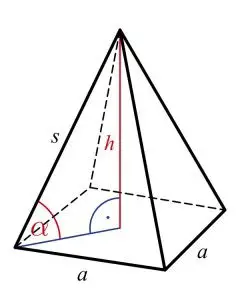 Hình chóp[/caption]

MỘT SỐ DẠNG TOÁN VỀ THỂ TÍCH HÌNH CHÓP THƯỜNG GẶP

Tìm thể tích hình chóp có cạnh bên nằm trên đường thẳng vuông góc với mặt phẳng chứa đa giác đáy

Đối với dạng bài tập này để tìm được thể tích hình chóp ta làm như sau:

• Xác định đường cao (chính là cạnh bên vuông góc với đáy).
• Tính đường cao và diện tích đáy
• Áp dụng công thức để tính thể tích hình chóp

Ví dụ minh họa

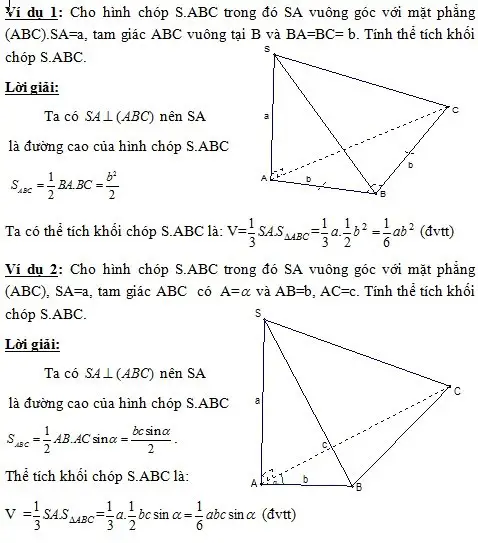
Tìm thể tích hình chóp có 2 mặt bên kề nhau cùng vuông góc với mặt đáy.

Đối với những dạng toán này ta làm như sau

• Xác định đường cao (chính là cạnh bên vuông góc với đáy).
• Tính đường cao và diện tích đáy
• Áp dụng công thức để tính thể tích hình chóp

Ví dụ minh họa

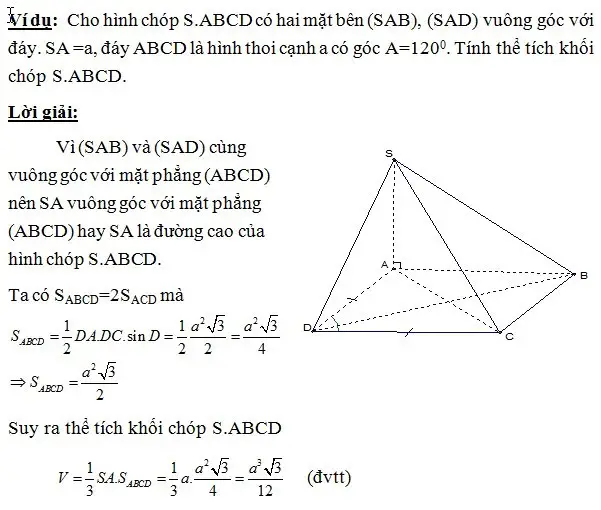
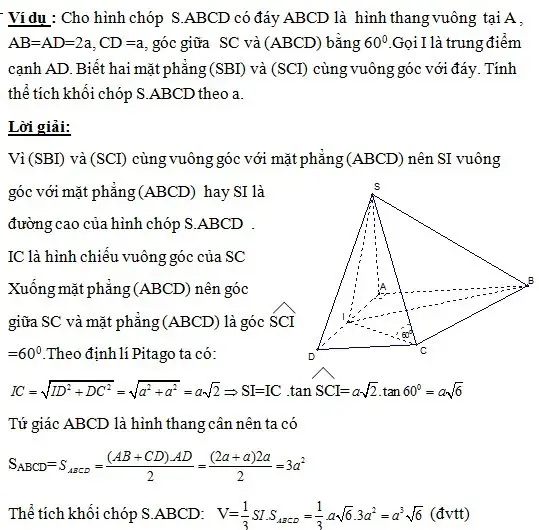
Hình chóp có hai mặt phẳng đi qua đỉnh (không chứa mặt bên) cùng vuông góc với mặt phẳng chứa đa giác đáy

• Xác định đường cao. (đường nằm trên giao tuyến của hai mặt phẳng cùng vuông góc với mặt đáy).
• Tính đường cao và diện tích đáy.
• Áp dụng công thức để tính thể tích khối chóp.

Vị dụ minh họa

Hình chóp có một mặt bên vuông góc với mặt đáy

• Xác định đường cao (đường hạ từ đỉnh xuống cạnh đáy là giao giữa mặt bên đó với mặt đáy.
• Tính đường cao và diện tích đáy.
• Áp dụng công thức để tính thể tích khối chóp.

Ví dụ minh họa

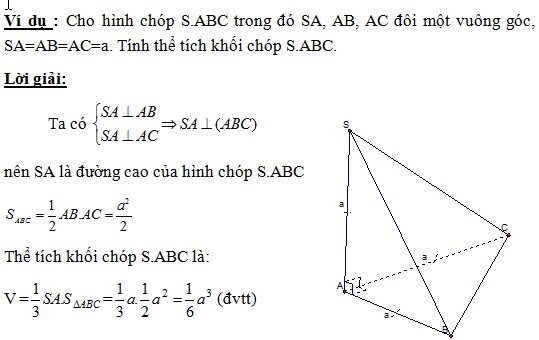
Tìm thể tích hình chóp có một cạnh bên vuông góc với hai đường thẳng cắt nhau thuộc mặt đáy

• Xác định đường cao (chính là cạnh bên vuông góc với hai đường thẳng cắt nhau thuộc mặt đáy).
• Tính đường cao và diện tích đáy.
• Áp dụng công thức để tính thể tích khối chóp.

Ví dụ minh họa

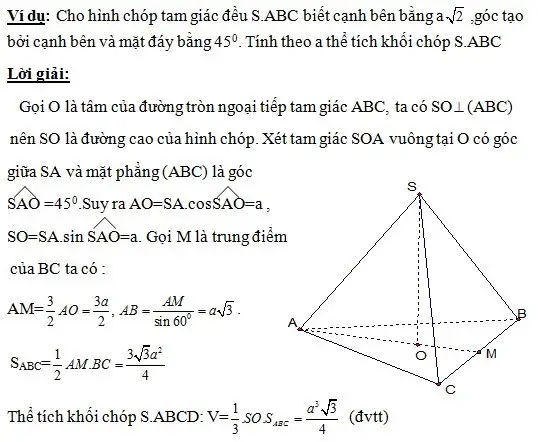
Tìm thể tích hình chóp đa giác đều

• Xác định đường cao (đường hạ từ đỉnh xuống tâm của đa giác đáy).
• Tính đường cao và diện tích đáy.
• Áp dụng công thức để tính thể tích khối chóp.

Ví dụ minh họa

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Tham khảo thêm bài nguyên mẫu tại đây : THỂ TÍCH HÌNH CHÓP

by via Học Dễ - Giúp bạn học tập dễ dàng hơn - Feed