HÀM SỐ BẬC NHẤT

KHÁI NIỆM VỀ HÀM SỐ

Nếu đại lượng y phụ thuộc vào đại lượng thay đổi x sao cho mỗi giá trị của x ta luôn xác định được chỉ một giá trị của y thì y được gọi là hàm số của x còn x được gọi là biến số.

Hàm số có thể được cho bằng bảng hoặc bằng công thức.

Giá trị của f(x) tại x₀ kí hiệu là f(x₀)

Đồ thị hàm số y = f(x) là tập hợp tất cả các điểm M (x;y) trong mặt phẳng tọa độ Oxy cho x, y thỏa mãn hệ thức y = f(x)

Hàm số đồng biến và hàm số nghịch biến. Cho hàm số y = f(x):

• Nếu x₁ < x₂ mà f(x₁) < f(x₂) thì hàm số y = f(x) đồng biến trên R
• Nếu x₁ < x₂ mà f(x₁) > f(x₂) thì hàm số y = f(x) nghịch biến trên R

ĐỊNH NGHĨA HÀM SỐ BẬC NHẤT Y = AX + B

Hàm số bậc nhất là hàm số được cho bởi công thức y = ax + b, trong đó a, b là những số cho trước và a ≠ 0.

Đặc biệt, khi b = 0 thì hàm số bậc nhất trở thành hàm số y = ax, biểu thị tương quan tỉ lệ thuận giữa y và x

TÍNH CHẤT HÀM SỐ BẬC NHẤT

Hàm số bậc nhất y = ax + b xác định với mọi giá trị của x thuộc R và có tính chất sau:

• Đồng biến trên R khi a > 0

Hàm số y = f(x) gọi là đồng biến trong khoảng nào đó nếu với mọi x1 và x2 trong khoảng đó sao cho x1 < x2 thì f(x1 ) < f(x2 )

• b) Nghịch biến trên R khi a < 0.

Hàm số y = f(x) gọi là nghịch biến trong khoảng nào đó nếu với mọi x1 và x2 trong khoảng đó sao cho x1 < x2 thì f(x1 ) > f(x2 )

Bảng biến thiên:

[caption id="attachment_2884" align="alignnone" width="679"]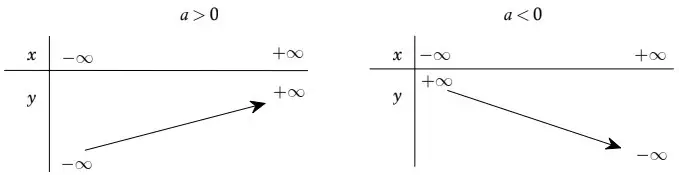 Bảng biến thiên[/caption]

CÁCH VẼ ĐỒ THỊ HÀM SỐ BẬC NHẤT Y = AX + B

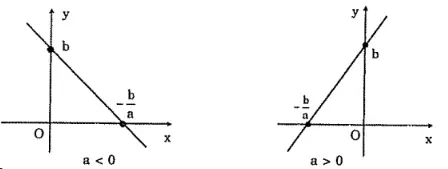
Trường hợp 1: Khi b=0

Trường hợp 2: Khi b khác 0

Ta cần xác định hai điểm phân biệt bất kì thuộc đồ thị.

• Bước 1: Cho x=0=>y=b. Ta được điểm P(0;b)∈Oy.

Cho y=0=>x=−ba. Ta được Q(−ba;0)∈0x.

• Bước 2: Vẽ đường thẳng đi qua hai điểm P và Q, ta được đồ thị của hàm số y=ax+b.

BÀI TẬP RÈN LUYỆN

 

 

 

 

 

 

 

 

 

 

 

 

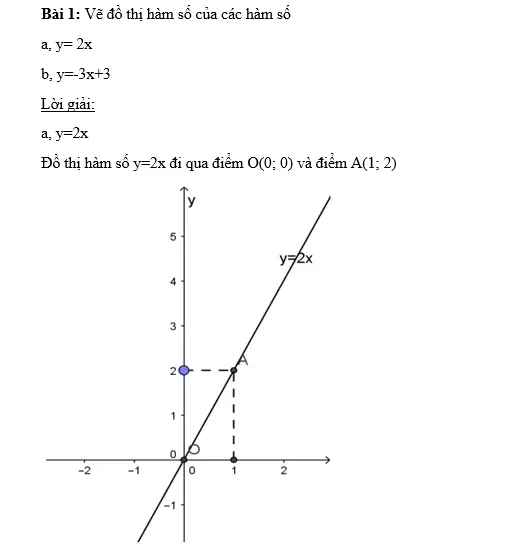
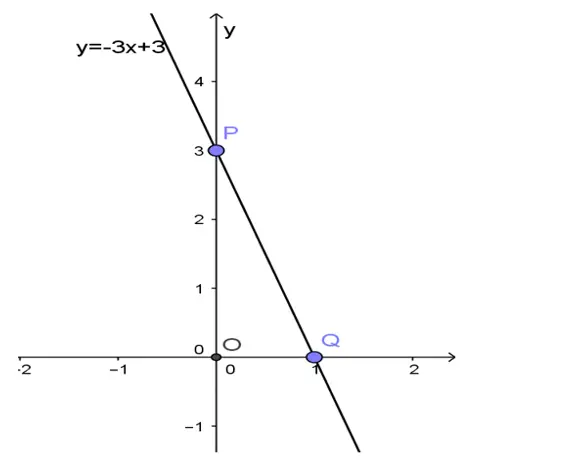
Đọc nguyên bài viết tại : HÀM SỐ BẬC NHẤT

by via Học Dễ - Giúp bạn học tập dễ dàng hơn - Feed