Kiến thức về hệ số góc của đường thẳng là kiến thức rất cơ bản mà các em sẽ được học trong chương trình học bậc THCS. Đây là kiến thức các em cần nắm vững để sau này tiếp tục học các chủ đề liên quan trong chương trình học bậc phổ thông như: phương trình đường thẳng và hệ số góc, hệ số góc của tiếp tuyến, viết phương trình tiếp tuyến khi biết hệ số góc,.. Bài viết dưới đây sẽ cung cấp cho các em kiến thức cơ bản nhất về hệ số góc từ khái niệm, định nghĩa đến cách tính hệ số góc như thế nào ? cuối bài sẽ có thêm phần bài tập vận dụng để các em có thể rèn luyện thêm sau bài học.
KHÁI NIỆM HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG
Định nghĩa 1: Hệ số góc của đường thẳng y=ax+b(a≠0) là hệ số của góc tạo thành (α) khi đường thẳng cắt trục hoành x′Ox tại một điểm và hợp với trục hoành x′Ox tạo thành một góc. Vì a trong phương trình hàm số có liên quan đến góc này nên a được gọi là hệ số góc của đường thẳng y=ax+b.
Đường thẳng y=ax+b đi qua điểm M(x0;y0) và có hệ số góc a có phương trình là y=a(x−x0)+y0
Hai đường thẳng song song hoặc trùng nhau sẽ có cùng hệ số góc.
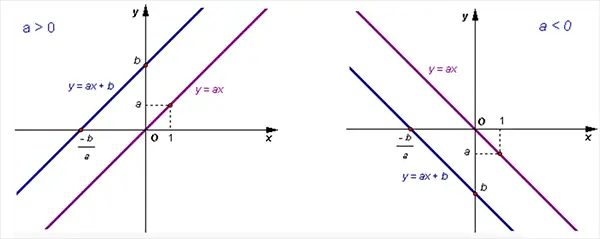
Khi a>0 thì góc tạo thành là góc nhọn, nằm bên trái trục tung Oy, và nếu a càng lớn thì góc đó càng lớn.
Khi a<0thì góc tạo thành là góc tù, nằm bên phải trục tung Oy và nếu a càng nhỏ thì góc đó càng lớn.
Khi a=0 thì không có hệ số góc vì khi đó đường thẳng y song song với trục hoành.
Như vậy ta thấy góc tạo bởi đường thẳng y=ax+b và trục Ox phụ thuộc vào a. Người ta gọi a là hệ số góc của đường thẳng y=ax + b.
Lưu ý:
- Khi a > 0, tan α = a
- Khi a < 0, tan (1800 - α) = - a. Ta tìm được số đo của góc 1800 - α rồi suy ra số đo của góc α
- Các đường thẳng có cùng hệ số a (a là hệ số của x) thì tạo với trục ox các góc bằng nhau.
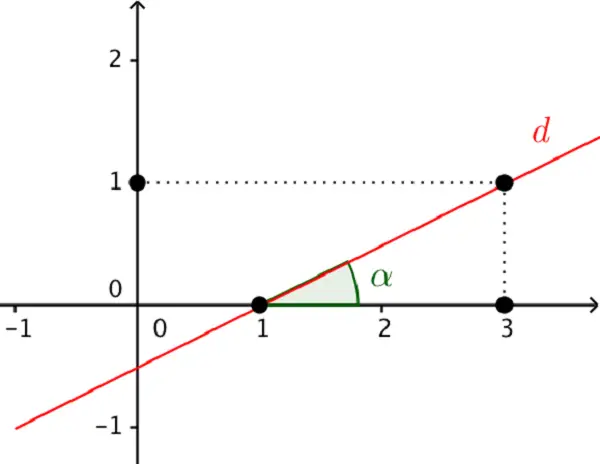
Định nghĩa 2: Đường thẳng không song song với trục tung có hệ số góc (slope) miêu tả độ dốc của đường thẳng và được định nghĩa là tỷ lệ sự thay đổi theo y so với sự thay đổi theo x của hai điểm bất kỳ nằm trên đường thẳng.
Như vậy nếu như đường thẳng đi qua hai điểm (x1, y1) và (x2, y2) thì hệ số góc của đường thẳng đó sẽ được tính bằng công thức ( x1 khác x2)
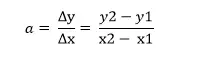
CÁCH TÍNH HỆ SỐ GÓC
Dạng tổng quát của đường thẳng y: Ax+By+C=0
Nếu B≠0 thì ta chuyển đường thẳng y về dạng như sau: y=ax+b ⇔ABx+y+CB=0⇔y=−ABx−CB
Khi đó hệ số góc của đường thẳng y là a = −AB.
Cách tính góc α tạo bởi đường thẳng y=ax+b và chiều dương trục Ox
Khi a>0, ta có:tanTAxˆ=OBOA=|b|∣∣−ba∣∣=|a|=a. Sau đó, sử dụng máy tính bỏ túi/ bảng lượng giác để suy ra số đo của TAxˆ.
Khi a<0, ta có: tan(180∘−TAxˆ)=tanOAPˆ=OPOA=|b|∣∣−ba∣∣=|a|=−a
Từ đó tìm ra được số đo của góc 180∘−TAxˆ
Suy ra số đo của TAxˆ.
BÀI TẬP RÈN LUYỆN
Bài tập 1
Cho hàm số y = mx+(2m+1) (1)
Với mỗi giá trị của m∈R , ta có một đường thẳng xác định bởi (1) . Như vậy, ta có một họ đường thẳng xác định bởi (1). Chứng minh rằng với mọi giá trị của m, họ đường thẳng xác định bởi (1) luôn đi qua một điểm cố định. Hãy xác định tọa độ của điểm đó.
Lời giải:
Chứng minh họ đường thẳng y=mx+(2m+1) (1) luôn đi qua một điểm cố định nào đó.
Giả sử điểm A(x0;y0) là điểm mà họ đường thẳng (1) đi qua với mọi m.
Khi đó tọa độ điểm A nghiệm đúng phương trình hàm số (1).
Với mọi m , ta có: y0=mx0+(2m+1)⇔(x0+2)m+(1−y0)=0
Vì phương trình nghiệm đúng với mọi giá trị của m nên tất cả các hệ số phải bằng 0.
Suy ra:
x0+2=0⇔x0=−21−y0=0⇔y0=1
Vậy A(−2;1) là điểm cố định mà họ đường thẳng y=mx+(2m+1) luôn đi qua với mọi giá trị m.
Bài tập 2
- Tìm hệ số góc của đường thẳng đi qua gốc tọa độ và đi qua điểm A(2; 1)
- Tìm hệ số góc của đường thẳng đi qua gốc tọa độ và đi qua điểm B(1; -2)
- Vẽ đồ thị của các hàm số với hệ số góc tìm được ở câu a, b trên cùng một mặt phẳng tọa độ và chứng tỏ rằng hai đường thẳng đó vuông góc với nhau.
Đáp án :
Đường thẳng đi qua gốc tọa độ có dạng y = ax + b
- Vì đường thẳng y = ax đi qua điểm A(2; 1) nên tọa độ điểm A nghiệm đúng phương trình đường thẳng.
Ta có: 1 = a.2 ⇔ a = 1/2
Vậy hệ số góc của đường thẳng đi qua gốc tọa độ và đi qua điểm A(2; 1) là a = 1/2
- Vì đường thẳng y = ax đi qua điểm B(1; -2) nên tọa độ điểm B nghiệm đúng phương trình đường thẳng.
Ta có: -2 = a.1 ⇔ a = -2
Vậy hệ số góc của đường thẳng đi qua gốc tọa độ và đi qua điểm B(1; -2) là a = -2
- Với a = 1/2 ta có hàm sô: y = 1/2.x
Với a = -2 ta có hàm số: y = -2x
*Vẽ đồ thị hàm số y = 1/2.x
Cho x = 0 thì y = 0. Ta có: O(0; 0)
Cho x = 2 thì y = 1. Ta có: A(2; 1)
Đồ thị hàm số y = 1/2.x đi qua O và A
*Vẽ đồ thị hàm số y = -2x
Cho x = 0 thì y = 0. Ta có: O(0; 0)
Cho x = 1 thì y = -2. Ta có: B(1; -2)
Đồ thị hàm số y = -2x đi qua O và B.
*Gọi A’, B’ lần lượt là hình chiếu của A, B trên Ox và Oy.
Ta có hai tam giác AA’O và BB’O có hai cạnh góc vuông tương ứng bằng nhau nên chúng bằng nhau.
 Khối trụ[/caption]
Khối trụ[/caption]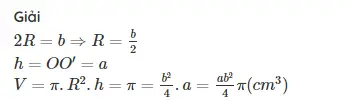
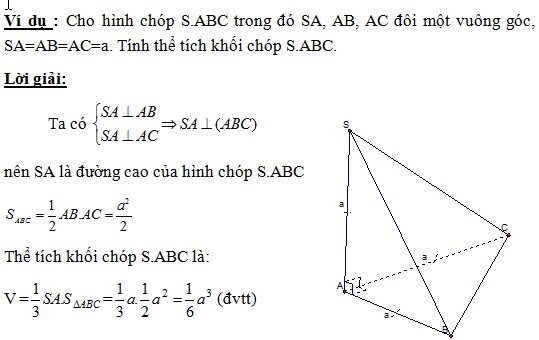
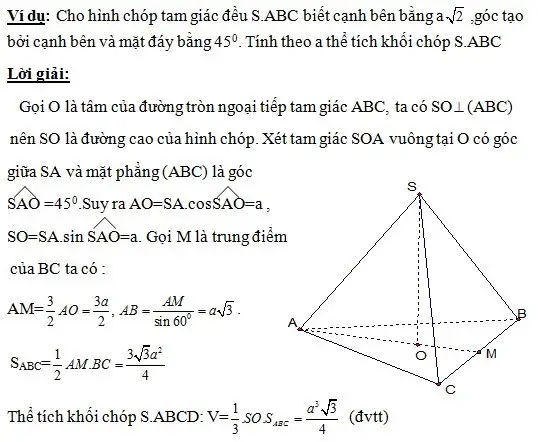
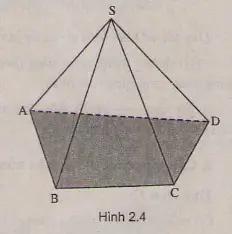 Hình chóp[/caption]
Hình chóp[/caption]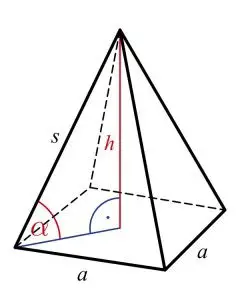 Hình chóp[/caption]
Hình chóp[/caption]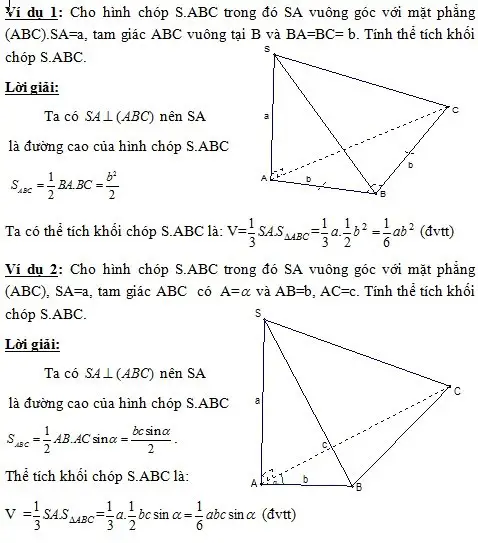
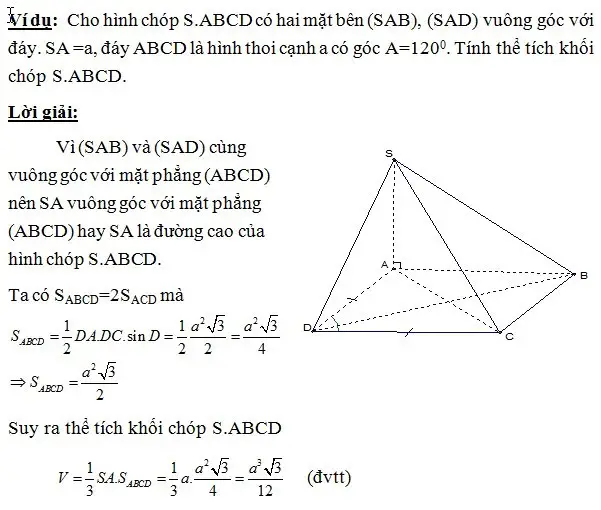


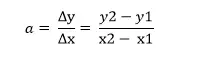

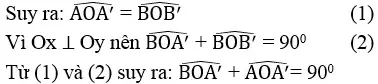 Vậy OA ⊥ OB hay hai đường thẳng y = 1/2.x và y = -2x vuông góc với nhau.
Vậy OA ⊥ OB hay hai đường thẳng y = 1/2.x và y = -2x vuông góc với nhau.
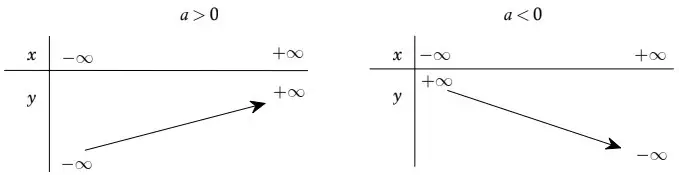 Bảng biến thiên[/caption]
Bảng biến thiên[/caption]

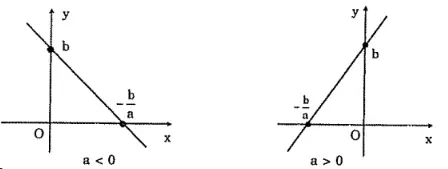 Trường hợp 2: Khi b khác 0
Trường hợp 2: Khi b khác 0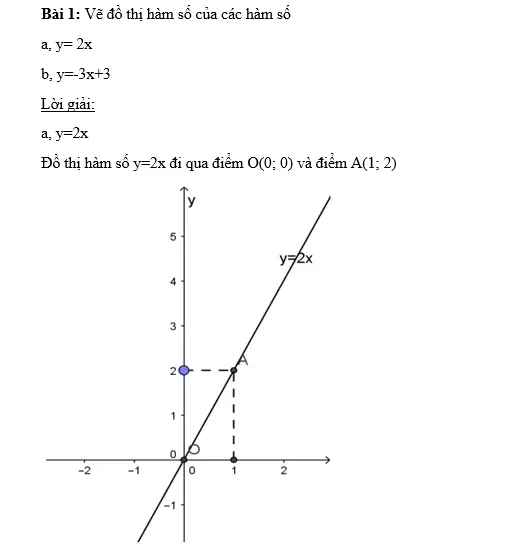






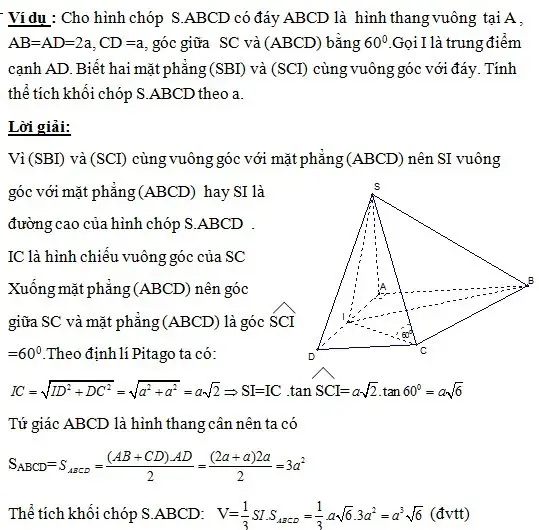
 Hình thang vuông[/caption]
Hình thang vuông[/caption]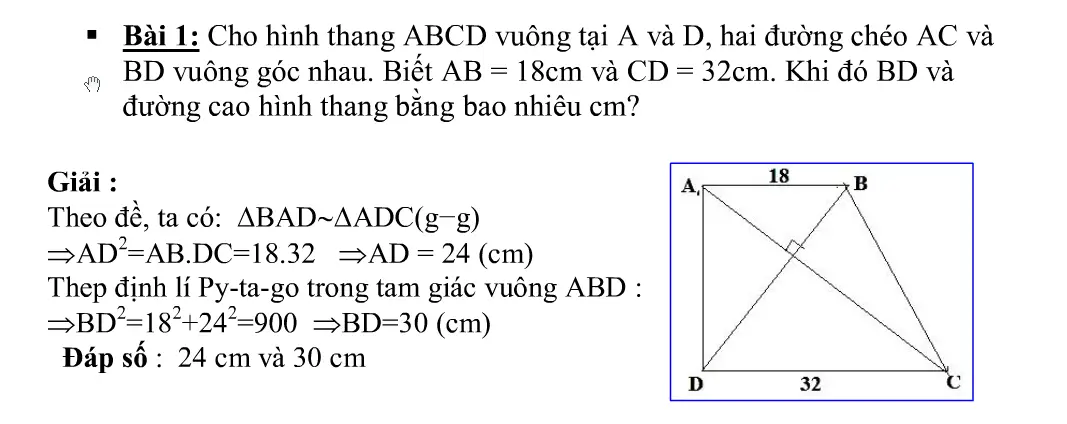 Bài tập về hình thang vuông[/caption]
Bài tập về hình thang vuông[/caption]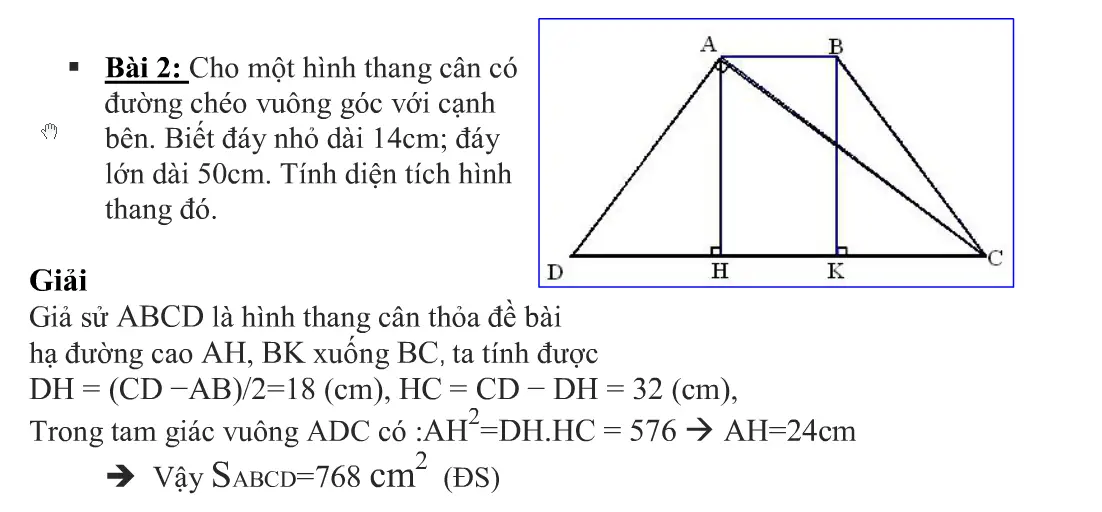 Bài tập về hình thang vuông[/caption]
Bài tập về hình thang vuông[/caption] Bài tập về hình thang vuông[/caption]
Bài tập về hình thang vuông[/caption]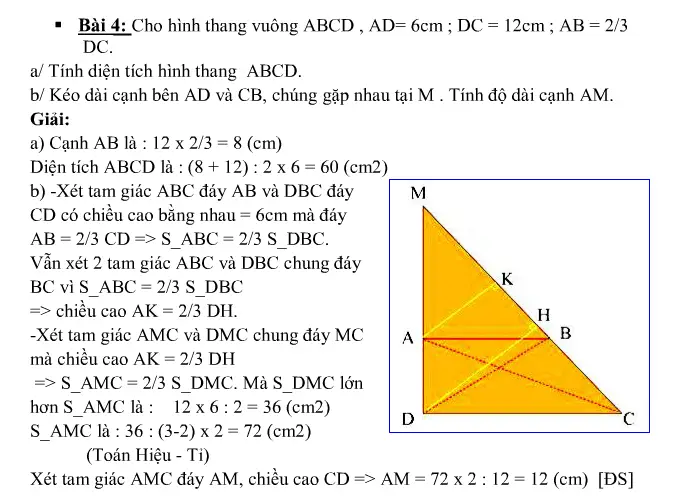 Bài tập về hình thang vuông[/caption]
Bài tập về hình thang vuông[/caption] ví dụ về phương pháp lập hệ phương trình[/caption]
ví dụ về phương pháp lập hệ phương trình[/caption]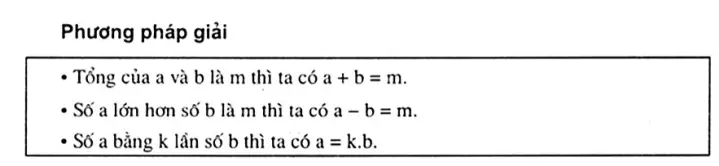
 Ví dụ về bài toán về quan hệ giữa các số[/caption]
Ví dụ về bài toán về quan hệ giữa các số[/caption] Ví dụ về bài toán về quan hệ giữa các số[/caption]
Ví dụ về bài toán về quan hệ giữa các số[/caption] Ví dụ về bài toán về quan hệ giữa các số[/caption]
Ví dụ về bài toán về quan hệ giữa các số[/caption] Dạng toán liên quan đến chữ số[/caption]
Dạng toán liên quan đến chữ số[/caption] Ví dụ về dạng toán liên quan đến chữ số[/caption]
Ví dụ về dạng toán liên quan đến chữ số[/caption] Ví dụ về dạng toán liên quan đến chữ số[/caption]
Ví dụ về dạng toán liên quan đến chữ số[/caption] Dạng toán làm chung công việc pp[/caption]
Dạng toán làm chung công việc pp[/caption] Dạng toán làm chung công việc bài tập[/caption]
Dạng toán làm chung công việc bài tập[/caption] Dạng toán làm chung công việc bài tập[/caption]
Dạng toán làm chung công việc bài tập[/caption] Dạng toán làm chung công việc bài tập[/caption]
Dạng toán làm chung công việc bài tập[/caption] Dạng toán làm chung công việc bài tập[/caption]
Dạng toán làm chung công việc bài tập[/caption] Dạng toán chuyển động[/caption]
Dạng toán chuyển động[/caption] Bài tập Dạng toán chuyển động[/caption]
Bài tập Dạng toán chuyển động[/caption]
 [/caption]
[/caption] Dạng toán có nội dung lý, hóa pp[/caption]
Dạng toán có nội dung lý, hóa pp[/caption] Bài tập Dạng toán có nội dung lý, hóa[/caption]
Bài tập Dạng toán có nội dung lý, hóa[/caption]
 Bài tập Dạng toán có nội dung lý, hóa[/caption]
Bài tập Dạng toán có nội dung lý, hóa[/caption] Bài tập giải bài toán bằng cách lập hệ phương trình[/caption]
Bài tập giải bài toán bằng cách lập hệ phương trình[/caption] Bài tập giải bài toán bằng cách lập hệ phương trình[/caption]
Bài tập giải bài toán bằng cách lập hệ phương trình[/caption] Bài tập giải bài toán bằng cách lập hệ phương trình[/caption]
Bài tập giải bài toán bằng cách lập hệ phương trình[/caption] Bài tập giải bài toán bằng cách lập hệ phương trình[/caption]
Bài tập giải bài toán bằng cách lập hệ phương trình[/caption] Bài tập giải bài toán bằng cách lập hệ phương trình[/caption]
Bài tập giải bài toán bằng cách lập hệ phương trình[/caption] Bài tập giải bài toán bằng cách lập hệ phương trình[/caption]
Bài tập giải bài toán bằng cách lập hệ phương trình[/caption]