Thứ Tư, 19 tháng 2, 2020

CÔNG THỨC CẤP SỐ NHÂN

ĐỊNH NGHĨA VỀ CẤP SỐ NHÂN

Cấp số nhân là một dãy số (hữu hạn hoặc vô hạn). Trong đó kể từ số hạng thứ 2, mỗi số hạn đều là tích của số hạng đứng ngay trước nó với số không đổi q. Số q gọi là công bội của cấp số nhân

[caption id="attachment_2820" align="alignnone" width="529"]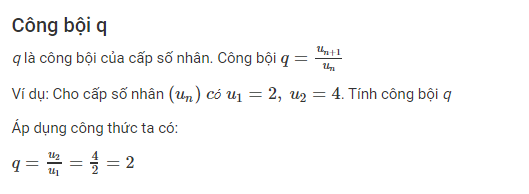Cấp số nhân và công bội q Cấp số nhân và công bội q[/caption]

Nếu (un) là cấp số nhân với công bội q, ta có un +1 = un.q, với mọi số nguyên dương n.

Tính chất của cấp số nhân

Định lí 1: Nếu (un) là một cấp số nhân thì kể từ số hạng thứ hai, bình phương của mỗi số hạng (trừ số hạng cuối đối với cấp số nhân hữu hạn) bằng tích của hai số hạng đứng kề nó trong dãy, tức là

[caption id="attachment_2821" align="aligncenter" width="169"]Định lý 1 Định lý 1[/caption]

[caption id="attachment_2822" align="alignnone" width="664"]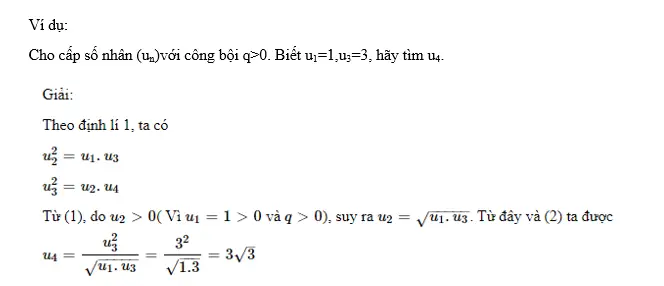Ví dụ về định lý 1 Ví dụ về định lý 1[/caption]

SỐ HẠNG CỦA CẤP SỐ NHÂN

Số hạng tổng quát của cấp số nhân

[caption id="attachment_2823" align="alignnone" width="655"]Số hạng tổng quát của cấp số nhân Số hạng tổng quát của cấp số nhân[/caption]

Tổng n số hạng đầu tiên của một cấp số nhân

[caption id="attachment_2824" align="alignnone" width="695"]Tổng n số hạng đầu tiên của một cấp số nhân Tổng n số hạng đầu tiên của một cấp số nhân

Tổng của cấp số nhân lùi vô hạn

Tổng của cấp số nhân lùi vô hạn
Tổng của cấp số nhân lùi vô hạn[/caption]

ví dụ về tổng của cấp số nhân lùi vô hạn

[caption id="attachment_2826" align="alignnone" width="809"]Ví dụ về tổng của cấp số nhân lùi vô hạn Ví dụ về tổng của cấp số nhân lùi vô hạn[/caption]

[caption id="attachment_2827" align="alignnone" width="445"]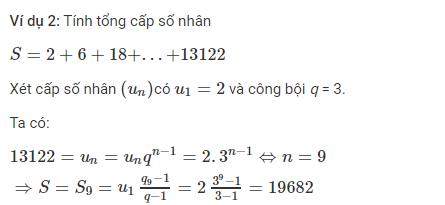Ví dụ về tổng của cấp số nhân lùi vô hạn 1Ví dụ về tổng của cấp số nhân lùi vô hạn 1 Ví dụ về tổng của cấp số nhân lùi vô hạn 1[/caption]

[caption id="attachment_2828" align="alignnone" width="663"]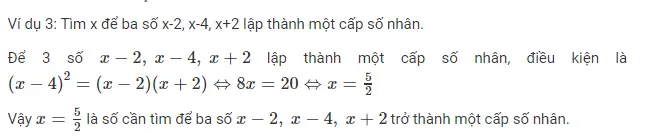Ví dụ về tổng của cấp số nhân lùi vô hạn 2 Ví dụ về tổng của cấp số nhân lùi vô hạn 2[/caption]

BÀI TẬP RÈN LUYỆN VỀ CẤP SỐ NHÂN

[caption id="attachment_2829" align="alignnone" width="696"]Bài tập về cấp số nhân Bài tập về cấp số nhân[/caption]

[caption id="attachment_2830" align="alignnone" width="703"]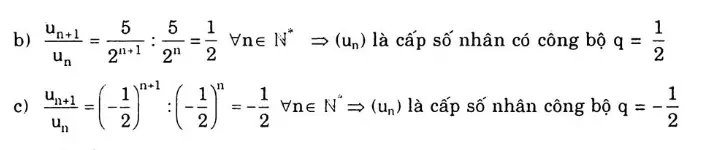Bài tập về cấp số nhân Bài tập về cấp số nhân[/caption]

[caption id="attachment_2831" align="alignnone" width="711"]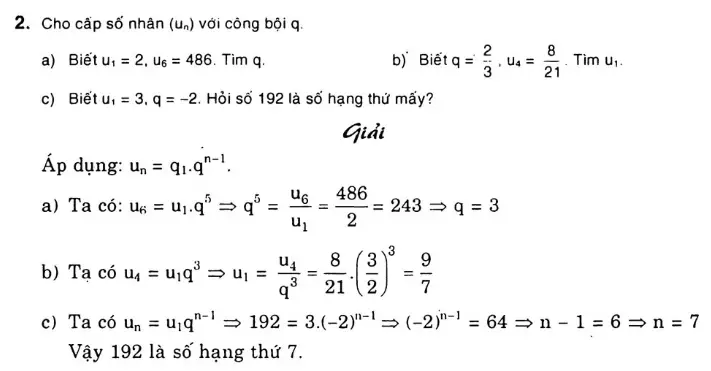Bài tập về cấp số nhân Bài tập về cấp số nhân[/caption]

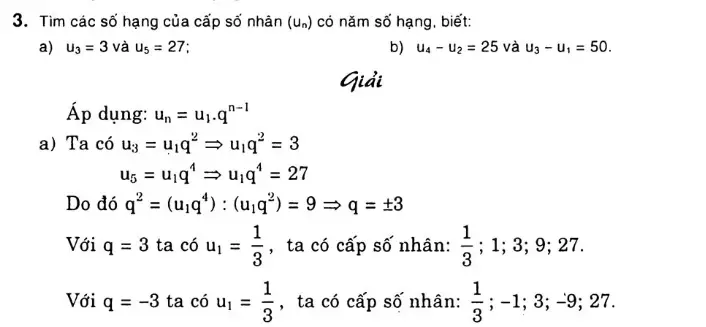
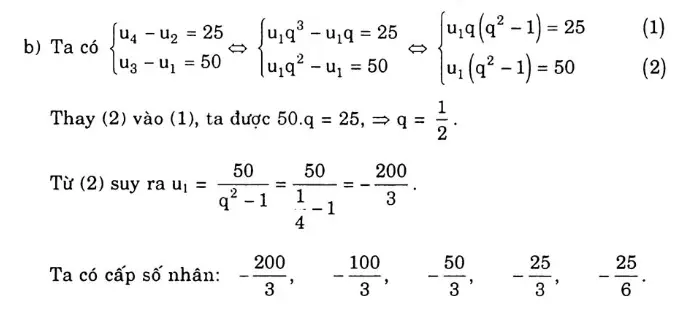
[caption id="attachment_2834" align="alignnone" width="706"]Bài tập về cấp số nhân

Bài tập về cấp số nhân
Bài tập về cấp số nhân[/caption]

 

[caption id="attachment_2836" align="alignnone" width="736"]Bài tập về cấp số nhân Bài tập về cấp số nhân[/caption]

[caption id="attachment_2837" align="alignnone" width="729"]Bài tập về cấp số nhân Bài tập về cấp số nhân[/caption]

 

 

 

 

 

 

 

 

 

 

 

Coi thêm tại : CÔNG THỨC CẤP SỐ NHÂN


by via Học Dễ - Giúp bạn học tập dễ dàng hơn - Feed
Người đăng: vào lúc Không có nhận xét nào:

TÌM HIỂU VỀ NHỊ THỨC NEWTON

NHỊ THỨC NEWTON

Định nghĩa về nhị thức newton

[caption id="attachment_2799" align="alignnone" width="658"]Định nghĩa về nhị thức Newton Định nghĩa về nhị thức Newton[/caption]

Tính chất của công thức nhị thức Newton

Tính chất của công thức nhị thức Newton

Một số kiến thức liên quan

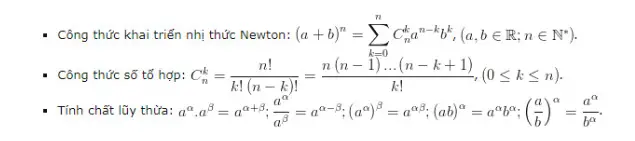BÀI TOÁN VỀ NHỊ THỨC NEWTON

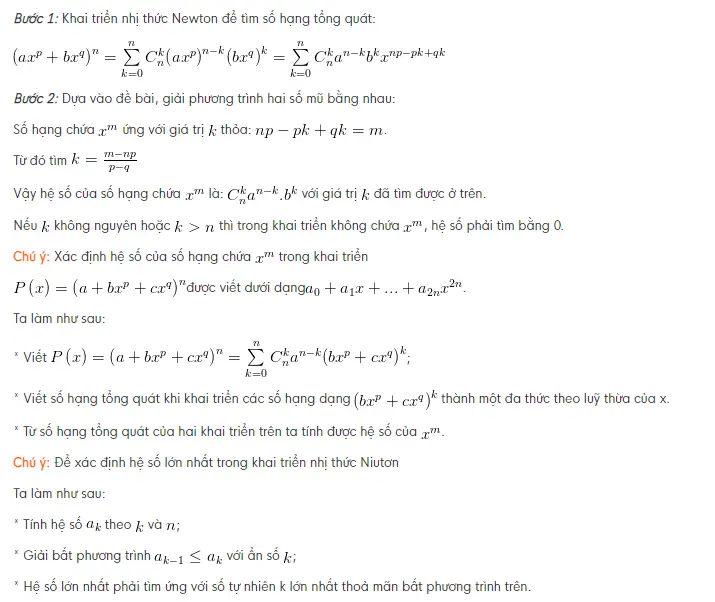Bài toán tìm số hạng thứ k trong khai triển nhị thức Newton

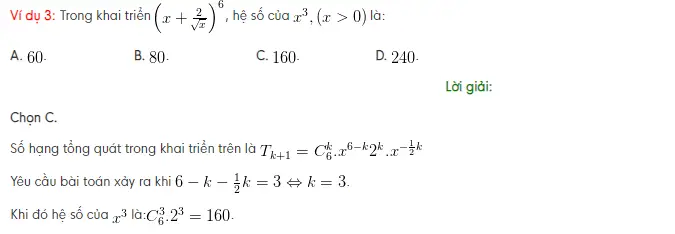[caption id="attachment_2804" align="alignnone" width="715"]Tìm số hạng thứ k trong khai triển nhị thức Newton Tìm số hạng thứ k trong khai triển nhị thức Newton[/caption]

[caption id="attachment_2805" align="alignnone" width="459"]Tìm số hạng thứ k trong khai triển nhị thức Newton Tìm số hạng thứ k trong khai triển nhị thức Newton[/caption]

[caption id="attachment_2806" align="alignnone" width="585"]Tìm số hạng thứ k trong khai triển nhị thức Newton Tìm số hạng thứ k trong khai triển nhị thức Newton[/caption]

[caption id="attachment_2807" align="alignnone" width="675"]Tìm số hạng thứ k trong khai triển nhị thức Newton Tìm số hạng thứ k trong khai triển nhị thức Newton[/caption]

Bài toán tính tổng, chứng minh đẳng thức

[caption id="attachment_2808" align="alignnone" width="615"]Bài toán tính tổng, chứng minh đẳng thức Bài toán tính tổng, chứng minh đẳng thức[/caption]

Bài toán ứng dụng nhị thức newton trong các bài liên quan đến tổ hợp

[caption id="attachment_2810" align="alignnone" width="471"]Bài toán ứng dụng nhị thức newton trong các bài liên quan đến tổ hợp Bài toán ứng dụng nhị thức newton trong các bài liên quan đến tổ hợp[/caption]

Bài toán về phương trình, bất phương trình chứa tổ hợp

[caption id="attachment_2811" align="alignnone" width="588"]Bài toán về phương trình, bất phương trình chứa tổ hợp Bài toán về phương trình, bất phương trình chứa tổ hợp[/caption]

BÀI TẬP RÈN LUYỆN

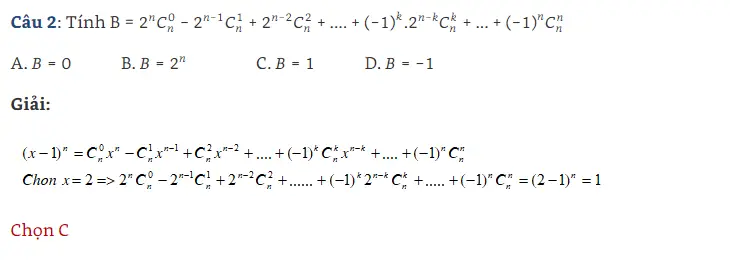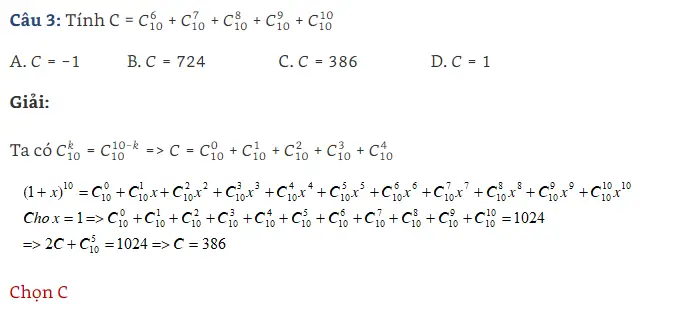[caption id="attachment_2812" align="alignnone" width="509"]Bài tập rèn luyện về nhị thức Newton Bài tập rèn luyện về nhị thức Newton[/caption]

[caption id="attachment_2813" align="alignnone" width="730"]Bài tập rèn luyện về nhị thức Newton Bài tập rèn luyện về nhị thức Newton[/caption]

[caption id="attachment_2814" align="alignnone" width="685"]Bài tập rèn luyện về nhị thức Newton Bài tập rèn luyện về nhị thức Newton[/caption]

[caption id="attachment_2815" align="alignnone" width="649"]Bài tập rèn luyện về nhị thức NewtonBài tập rèn luyện về nhị thức Newton Bài tập rèn luyện về nhị thức Newton[/caption]

[caption id="attachment_2816" align="alignnone" width="831"]Bài tập rèn luyện về nhị thức Newton Bài tập rèn luyện về nhị thức Newton[/caption]

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Xem thêm bài nguyên mẫu tại : TÌM HIỂU VỀ NHỊ THỨC NEWTON


by via Học Dễ - Giúp bạn học tập dễ dàng hơn - Feed
Người đăng: vào lúc Không có nhận xét nào:

SỐ CHÍNH PHƯƠNG LÀ GÌ ?

Số chính phương  là một số tự nhiên có căn bậc 2 cũng là một số tự nhiên. Bản chất của số chính phương là bình phương của một số tự nhiên nào đó. Số chính phương là thể hiện diện tích của một hình vuông với chiều dài là cạnh số nguyên kia.

Ví dụ: 4 = 2², 9 = 3²

Số chính phương hiển thị diện tích của một hình vuông có chiều dài cạnh bằng số nguyên kia.

Các tính chất của số chính phương

  • Số chính phương có thể tận cùng bằng 0;1;4;5;6;9.Không thể tận cùng bằng 2,3,7,8

[caption id="attachment_2763" align="aligncenter" width="604"]Bảng số tận cùng số chính phương Số tận cùng một số chính phương[/caption]

  • Tính chia hết
    • Số chính phương khi chia cho 3 chỉ có số dư là 0 hoặc 1
    • Số chính phương chẵn thì chia hết cho 4, số chính phương lẻ chia 4 dư 1 hoặc 3
    • Số chính phương khi chia cho 5 chỉ có số dư là 0; 1 hoặc là -1 (hay dư 4)

[caption id="attachment_2764" align="alignnone" width="521"]Chứng minh số chính phương chia 3 dư 0 hoặc 1 Chứng minh số chính phương chia 3 dư 0 hoặc 1[/caption]

  • Khi phân tích một số chính phương ra thừa số nguyên tố ta được các thừa số là lũy thừa của số nguyên tố với mũ chẵn
  • Số chính phương chia cho 4 hoặc 3 không có số sư là 2. Số chính phương lẻ khi chia 8 luôn dư 1
  • Số ước nguyên dương của số chính phương là một số lẻ
  • Số chính phương chia hết cho số nguyên tố p thì chia hết cho p2

[caption id="attachment_2765" align="alignnone" width="474"]Tính chia hết của một số chính phương Ví dụ về tính chia hết[/caption]

  • Giữa hai số chính phương liên tiếp không tồn tại số chính phương nào

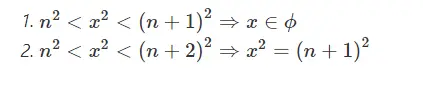[caption id="attachment_2766" align="aligncenter" width="423"]Tính chất của một số chính phương Ví dụ về tính chất của một số chính phương[/caption]

  • Nếu hai số nguyên liên tiếp có tích là một số chính phương thì một trong hai số đó bằng 0
  • Tất cả các số chính phương có thể viết thành dãy tổng của các số lẻ tăng dần từ 1

[caption id="attachment_2767" align="aligncenter" width="312"]Tính chất số chính phương 1 Ví dụ về tính chất của một số chính phương[/caption]

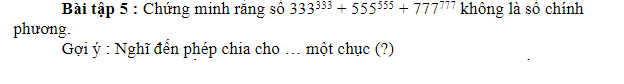Một số bài tập về số chính phương

[caption id="attachment_2768" align="alignnone" width="661"]Bài tập về số chính phương bài 1 Bài tập về số chính phương[/caption]

[caption id="attachment_2769" align="alignnone" width="659"]Bài tập về số chính phương Bài tập về số chính phương bài 2[/caption]

[caption id="attachment_2770" align="alignnone" width="681"]Bài tập về số chính phương Bài tập về số chính phương bài 3[/caption]

[caption id="attachment_2771" align="alignnone" width="669"]Bài tập về số chính phương Bài tập về số chính phương bài 4[/caption]

[caption id="attachment_2775" align="alignnone" width="624"]Bài tập về số chính phương Bài tập về số chính phương bài 5[/caption]

 

[caption id="attachment_2773" align="alignnone" width="687"]Bài tập về số chính phương Bài tập về số chính phương bài 6[/caption]

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Coi thêm ở : SỐ CHÍNH PHƯƠNG LÀ GÌ ?


by via Học Dễ - Giúp bạn học tập dễ dàng hơn - Feed
Người đăng: vào lúc Không có nhận xét nào:

KIẾN THỨC VỀ LĂNG TRỤ TAM GIÁC ĐỀU

KIẾN THỨC VỀ HÌNH LĂNG TRỤ TAM GIÁC ĐỀU

Hình lăng trụ là một đa diện gồm có hai đáy là hai đa giác bằng nhau và nằm trên hai mặt phẳng song song, các mặt bên là hình bình hành, các cạnh bên song song hoặc bằng nhau

Hình lăng trụ tam giác đều là hình lăng trụ có hai đáy là hai tam giác đều bằng nhau.

 

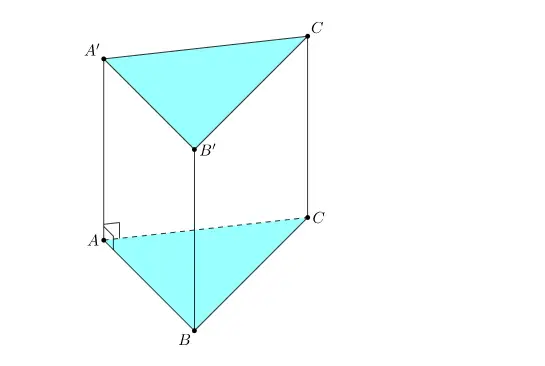[caption id="attachment_2783" align="aligncenter" width="545"]Hình lăng trụ tam giác đều, tính chất, công thức và bài tập về lăng trụ tam giác đều Hình lăng trụ tam giác đều[/caption]

Tính chất hình lăng trụ tam giác đều

Tính chất hình lăng trụ tam giác đêu:

  • Hai đáy là hai tam giác đều bằng nhau do đó các cạnh đáy bằng nhau.
  • Cạnh bên vuông góc với mặt đáy.
  • Các mặt bên là các hình chữ nhật.

Công thức tính thể tích của một lăng trụ tam giác đều

Thể tích hình lăng trụ bằng diện tích của mặt đáy và khoảng cách giữa hai mặt đáy hoặc là chiều cao. Công thức tính thể tích hình lăng trụ tam giác giác đều

V=B.h

Trong đó:B là diện tích đáy, h là chiều cao của khối lăng trụ, V là thể tích khối lăng trụ

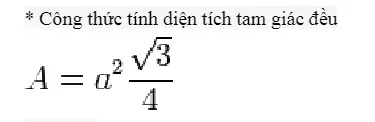Đáy của hình lăng trụ tam giác đều chính là hình tam giác đều. gọi A là diện tích của tam giác đều ta có công thức tính diện tích tam giác đều như sau:

[caption id="attachment_2784" align="aligncenter" width="375"]Công thức tính diện tích tam giác đều Công thức tính diện tích tam giác đều[/caption]

BÀI TẬP VẬN DỤNG

Bài tập 1

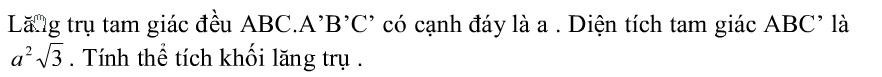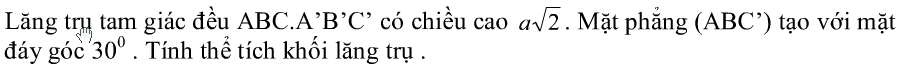[caption id="attachment_2785" align="alignnone" width="764"]Bài tập về lăng trụ tam giác đều Bài tập về lăng trụ tam giác đều[/caption]

Bài tập 2

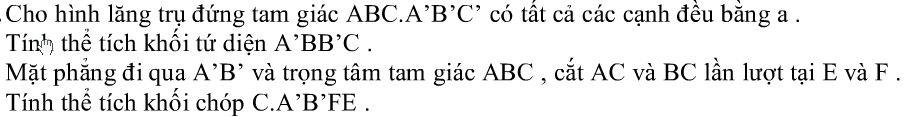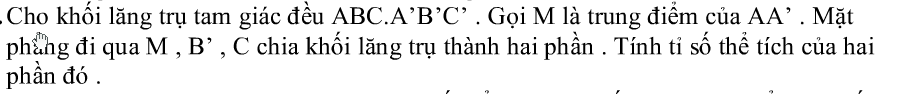[caption id="attachment_2786" align="alignnone" width="916"]Bài tập về lăng trụ tam giác đều Bài tập về lăng trụ tam giác đều[/caption]

Bài tập 3

[caption id="attachment_2787" align="alignnone" width="882"]Bài tập về lăng trụ tam giác đều Bài tập về lăng trụ tam giác đều[/caption]

Bài tập 4

[caption id="attachment_2788" align="alignnone" width="903"]Bài tập về lăng trụ tam giác đều Bài tập về lăng trụ tam giác đều[/caption]

Bài tập 5

[caption id="attachment_2789" align="alignnone" width="916"]Bài tập về lăng trụ tam giác đều Bài tập về lăng trụ tam giác đều[/caption]

Bài tập 6

[caption id="attachment_2790" align="alignnone" width="925"]Bài tập về lăng trụ tam giác đều Bài tập về lăng trụ tam giác đều[/caption]

Bài tập 7

[caption id="attachment_2791" align="alignnone" width="915"]Bài tập về lăng trụ tam giác đều Bài tập về lăng trụ tam giác đều[/caption]

Bài tập 8

[caption id="attachment_2792" align="alignnone" width="934"]Bài tập về lăng trụ tam giác đều Bài tập về lăng trụ tam giác đều[/caption]

Bài tập 9

[caption id="attachment_2793" align="alignnone" width="930"]Bài tập về lăng trụ tam giác đều Bài tập về lăng trụ tam giác đều[/caption]

Bài tập 10

[caption id="attachment_2794" align="alignnone" width="909"]Bài tập về lăng trụ tam giác đều Bài tập về lăng trụ tam giác đều[/caption]

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Đọc nguyên bài viết tại : KIẾN THỨC VỀ LĂNG TRỤ TAM GIÁC ĐỀU


by via Học Dễ - Giúp bạn học tập dễ dàng hơn - Feed
Người đăng: vào lúc Không có nhận xét nào:
Đăng ký: Bài đăng (Atom)