Là một quốc gia gắn liền với nền nông nghiệp trồng lúa nước, nên những con sông trải dài trên khắp lãnh thổ Việt Nam trở thành một nét đẹp văn hóa trong đời sống của người dân ta. Trong bài viết này, chúng tôi sẽ giới thiệu đến các em những bài văn mẫu miêu tả dòng sông quê hương được tuyển chọn trong sách văn mẫu lớp 5 giúp các em có thể làm tốt hơn bài văn này nhé!
Gợi ý lập dàn ý miêu tả dòng sông
1. Mở bài
Giới thiệu dòng sông quê em: tên của dòng sông (nếu có), dòng sông đó ở nơi em sinh sống hay ở quê nội, quê ngoại?
2. Thân bài
Miêu tả về dòng sông:
- Hình dáng của dòng sông
- Hai bên bờ dòng sông
- Nước của dòng sông theo mùa thay đổi như thế nào
- Đời sống sinh vật dưới dòng sông ra sao
Miêu tả về đời sống con người quê em gắn liền với dòng sông:
- Dòng sông cho tôm cá với hình ảnh thân thuộc của bác nông dân kéo chài, kéo lưới.
- Ở mỗi bến nước người dân thường giặt giũ, ngồi hóng mát dưới gốc cây.
- Mỗi buổi chiều mùa hè trẻ em và người lớn tắm sông, nô đùa vui vẻ.
3. Kết bài
Nói về tình cảm của em với dòng sông quê hương.
Những bài văn mẫu hay miêu tả dòng sông
1. Bài văn miêu tả dòng sông số 1
Vậy là một năm học cũng đã trôi qua, bố mẹ lại đưa em về quê nội thăm ông bà. Ngày mai em được về quê rồi, cả đêm em háo hức không ngủ được vì mong gặp ông bà cũng rất nhớ dòng sông quê hương.

Hình ảnh dòng sông quen thuộc
Về quê có rất nhiều điều mới lạ để em khám phá và một trong những điều ấy chính là dòng sông quê. Quê nội em cũng như bao làng quê khác ở Việt Nam có lũy tre làng có dòng sông uốn lượn chảy quanh. Dòng sông này gắn liền với tuổi thơ của bố em, là nơi bố em đã sinh ra và lớn lên.
Em cũng không biết nguồn gốc của dòng sông này bắt đầu từ đâu, người dân quê em gọi nó bằng một cái tên thân thương: sông Đò. Dòng sông Đò như 1 dải lụa đào uốn lượn chảy quanh ngôi làng vô cùng mềm mại. Một bên của dòng sông là cánh đồng lúa thẳng cánh cò bay và một bên là đường làng em.
Buổi sáng sớm, dòng sông lặng im và trầm ngâm trước tiếng gáy vang ò ó o của những chú gà trống, phản chiếu ánh nắng đang lên của ông mặt trời. Buổi trưa hè, khi ông mặt trời đã lên cao, dòng sông lúc này nước chảy lăn tăn hơi gợn sóng và lấp lánh như được phủ hàng ngàn viên pha lê trên bề mặt sông. Còn buổi chiều tà dòng sông lại trở nên sôi động, nhộn nhịp với đời sống của người dân làng. Buổi tối dòng sông tĩnh mĩnh, chỉ thi thoảng vang vọng tiếng ếch tiếng nhái kêu hay tiếng gõ mạn thuyền của bác thuyền chài.
Dưới lòng sông là một thế giới sinh vật vô cùng đa dạng, phong phú với tôm với cá. Thi thoảng em nhìn thấy những chú cá bơi lượn sát mặt nước vô cùng sinh động, hay có những chú cá tinh nghịch còn nhảy hẳn lên mặt nước làm bắn tung những giọt nước nhỏ. Trôi lững lờ trên bề mặt dòng sông là những cây lục bình với hoa màu tím bắt mắt. Thi thoảng ở hai bên bờ sông, người dân còn tạo những bè rau muống dùng làm thức ăn cho heo.
Ông em bảo rằng, đời sống của dân làng từ xưa đến nay đều gắn liền với dòng sông này. Sông cho nước tưới tiêu cho ruộng đồng, nuôi lớn những cây lúa là hạt ngọc của trời đất, cho người dân của lương thực để ăn. Sông cho cá cho tôm để những bữa ăn của người dân thêm đậm đà, đủ chất và nhiều gia đình chài lười còn sống nhờ tôm cá của dòng sông.
Dòng sông còn là nơi cứ mỗi buổi chiều tà, phụ nữ thì ngồi trên bờ giặt giũ nói chuyện, trẻ em đàn ông sẽ xuống sông tắm mát và nô đùa vui vẻ. Những khung cảnh yên bình, thú vị này em chỉ có thể được tận mắt nhìn và được trải nghiệm khi về quê nội mà thôi. Em cũng được bố cho xuống sông tắm. Cảm giác được hòa mình vào dòng sông quê mát lạnh thật sự khiến em thích thú và nhớ mãi. Dường như cái oi ả mùa hè đều tan biến tại dòng sông quê.
Lần này về quê em đã nhờ bố chuẩn bị cả máy ảnh để em có thể lưu giữ những bức hình về dòng sông Đò quê em.
2. Bài văn miêu tả dòng sông số 2
Sinh ra và lớn lên ở làng quê Việt Nam, tuổi thơ của em gắn liền với cánh đồng lúa, với cánh diều vi vu và với dòng sông thân thuộc. Dòng sông quê em giống như một người mẹ hiền bao đời chăm lo cho những đứa con thôn làng.
Dòng sông quê em là một nhánh nhỏ của con sông Hồng đỏ nặng phù sa. Dòng sông như mái tóc mượt mà của người thiếu nữ uốn lượn và chảy quanh ngôi làng, bao bọc lấy ngôi làng của em. Em không biết dòng sông này chảy qua những đâu, nhưng chắc chắn rằng nó phải chảy qua rất nhiều xóm làng, qua rất nhiều cánh đồng xanh, qua rất nhiều bãi đồi.

Dòng sông quê hương gắn liền với tuổi thơ
Mỗi mùa, dòng sông như thay một chiếc áo mới vô cùng sinh động. Mùa hè nước trong và sáng lấp lánh nhờ phản chiếu ánh mặt trời. Mùa thu nước sông lại trong vắt và yên bình. Mua đông dòng sông lại trầm ngâm mang một vẻ đẹp rất riêng. Còn mùa xuân, dòng sông như bừng tỉnh sau một giấc ngủ dài với nguồn sống dồi dào. Đặc biệt vào mùa hè, khi những cơn mưa rào đổ xuống, dòng sông có màu đỏ do đất cát, phù sa chảy xuống. Nhưng cũng rất nhanh chóng sau vài hôm khi mưa đã tạnh, nước dòng sông lại trở nên trong vắt.
Em rất thích được ngắm dòng sông vào buổi sáng sớm tinh mơ. Khi ấy em được nhìn những chú cá đi kiếm ăn, được nhìn những con ốc bám trên những thân cây khoai, thân rau muống mà chỉ cần chạm nhẹ chúng sẽ thu mình vào trong chiếc vỏ để chìm xuống. Vào sáng sớm cũng là lúc bắt đầu đi kiếm ăn của đàn vịt bơi tung tăng, của những chú bói cá sắc màu sặc sỡ. Một bên bờ sông là đường làng, người người hối hả bắt đầu nhiệm vụ ngày mới của mình: bác nông dân ra đồng, các bạn học sinh đi học, người đi chợ, người đi làm…Cùng với những rặng cây bên bờ sông, tất cả tạo nên một bức tranh vô cùng sinh động.
Vào mùa hè, mỗi buổi chiều em cùng lũ trẻ trong xóm đều ra bến nước đầu làng dưới gốc đa để tắm sông. Dòng sông như một người mẹ hiền ôm lấy chúng em, cho chúng em thỏa sức nô đùa. Trong khi đó, những bác nông dân đi làm về tranh thủ nghỉ mát dưới gốc đa, những bà những mẹ lại tranh thủ giặt đồ.
Có lẽ sông chỉ thực sự yên tĩnh và ban đêm khi trăng đã lên. Dòng sông phải chiếu ánh trăng lung linh và thơ mộng vô cùng. Ông trăng lặn sâu xuống đáy sông tạo nên một khung cảnh khiến những ai có tâm hồn thi sĩ có thể xuất khẩu thành thơ.
Em rất yêu dòng sông quê em. Sau này dù lớn lên có đi đâu xa, em vẫn sẽ mãi lưu giữ bóng hình quê hương với dòng sông tuổi thơ.
3. Bài văn miêu tả dòng sông số 3
Mặc dù sinh ra ở quê, nhưng khi em bắt đầu vào lớp 1, bố mẹ chuyển công tác lên thành phố, em cũng theo bố mẹ lên thành phố sống từ đó. Mặc dù đã sống ở nơi thành thị tấp nập vài năm, nhưng mỗi lần nghỉ hè được về quê em vẫn vô cùng mong đợi và háo hức. Bởi em nhớ ông bà, nhớ làng xóm và đặc biệt nhớ dòng sông quê hương.
Dù có đi đâu, có thấy bao nhiêu dòng sông, em vẫn thấy con sông quê em là con sông đẹp nhất. Dòng sông bắt nguồn từ những con suối rừng Trường Sơn hùng vĩ. Sông chảy qua biết bao vùng đất, qua nhiều ruộng đồng, qua nhiều bãi bồi và lặng lẽ, trầm ngâm khi tới làng em. Ngay bên cạnh dòng sông là con đường chính của làng, vì thế bất cứ ai đi đâu hay về làng đều đi qua con đường bên cạnh dòng sông này.
Nhìn từ xa, con sông quê em giống như một con trăn khổng lồ uốn lượn quanh làng. Dòng sông dài bao nhiêu em không biết và cả các bô lão trong làng em cũng không biết được. Chỗ rộng nhất của dòng sông khi chảy qua làng em cũng chỉ khoảng vài mét mà thôi.

Dòng sông hiền hoà như một người mẹ
Nước của dòng sông được thay đổi theo mùa. Vào mùa khô, nước sông cạn và trong vắt dường như có thể nhìn thấy cả đáy với từng đàn cá tung tăng bơi lội. Vào mùa mưa, nước sông dâng cao và đổi màu thành màu đục. Đặc biệt, những đợt lũ đổ về, nước sông đỏ ngầu và giận giữ vô cùng đáng sợ. Thế nhưng, khi lũ đã qua đi, dòng sông lại trở về sự hiền hòa như một người mẹ hiền.
Dòng sông cung cấp nước cho ruộng đồng, như nguồn sữa mẹ nuôi lớn những cây lúa, cây khoai cây ngô cho người dân quê em có nguồn lương thực dồi dào. Không chỉ vậy, dưới lòng sông còn có cả một thế giới sinh vật phong phú từ tôm, cá, cua, ốc, trai… Hàng ngày, các bác thuyền chài nhẹ lướt con thuyền trên dòng sông để thả lưới bắt cá bắt tôm. Ông em bảo việc thả lưới được nhiều cá tôm hay không còn tùy vào con nước mà chỉ người có kinh nghiệm lâu năm mới biết được.
Hai bên bờ sông được dân làng trồng những cây cao lớn như cây liễu, cây phượng, cây bàng soi bóng xuống dòng sông. Nhưng đặc biệt nhất và trở thành nét đẹp, linh hồn làng quê có lẽ là cây đa cổ thụ cùng bến nước ngay đầu làng. Nghe nói, cây đa này được cụ tổ khai sinh ra làng trồng từ nhiều năm về trước. Mỗi khi đi làm đồng về, người dân quê em đều dừng lại ở đây rửa tay chân và ngồi dưới gốc đa nghỉ mát.
Đã là một đứa trẻ sinh ra ở làng quê với tuổi thơ gắn liền với dòng sông có lẽ chẳng một ai chưa từng tắm sông. Mỗi buổi chiều hè, lũ trẻ trong xóm lại rủ nhau tắm sông và nô đùa. Nước sông mát lành xua tan cái oi ả mùa hè và cả một khúc sông vang những tiếng cười giòn tan của lũ trẻ chúng em.
Dòng sông quê hương như một nét đẹp tuổi thơ mà đi đâu em cũng sẽ luôn nhớ về. Em rất yêu dòng sông quê em.
Trên đây là những bài văn mẫu miêu tả dòng sông hay, các em hãy tham khảo và tự viết một bài văn miêu tả dòng sông của mình nhé. Chúc các em đạt điểm cao!
Tham khảo thêm bài nguyên mẫu tại đây : Bài văn miêu tả dòng sông quê hương em- văn mẫu lớp 5
by via Học Dễ - Giúp bạn học tập dễ dàng hơn - Feed
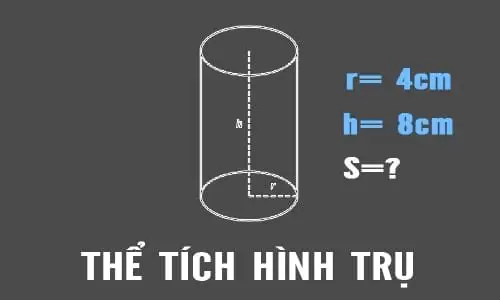
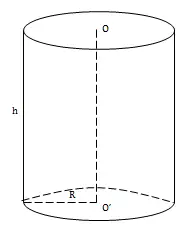 Khối trụ[/caption]
Khối trụ[/caption]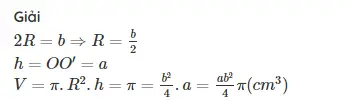
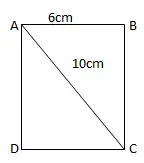
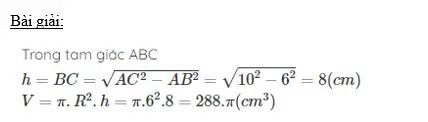
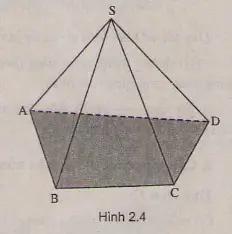 Hình chóp[/caption]
Hình chóp[/caption]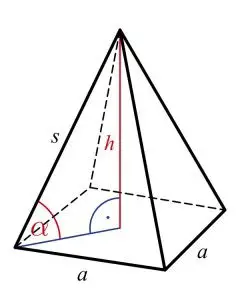 Hình chóp[/caption]
Hình chóp[/caption]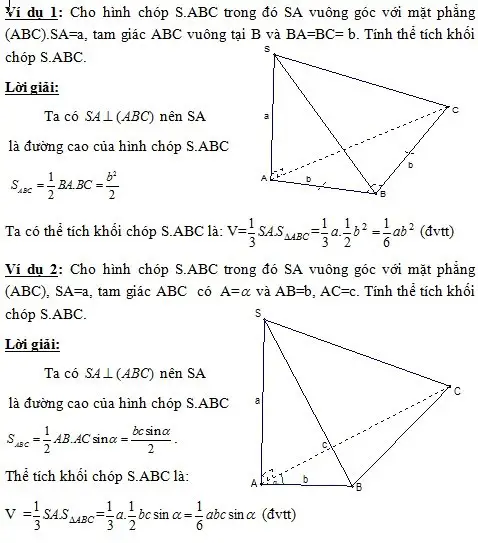

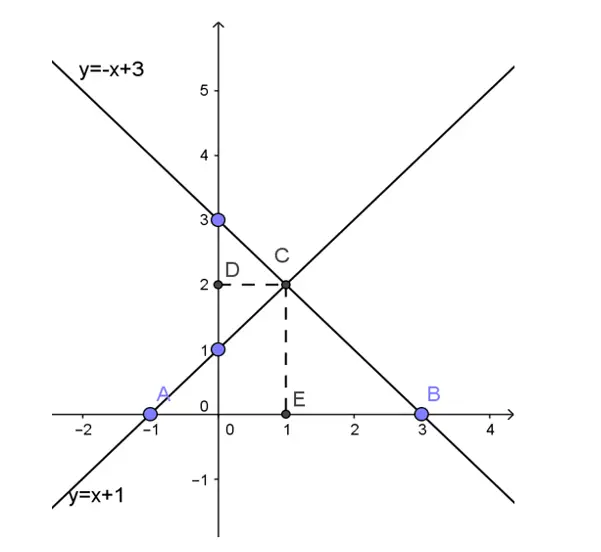
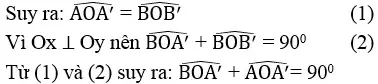 Vậy OA ⊥ OB hay hai đường thẳng y = 1/2.x và y = -2x vuông góc với nhau.
Vậy OA ⊥ OB hay hai đường thẳng y = 1/2.x và y = -2x vuông góc với nhau.
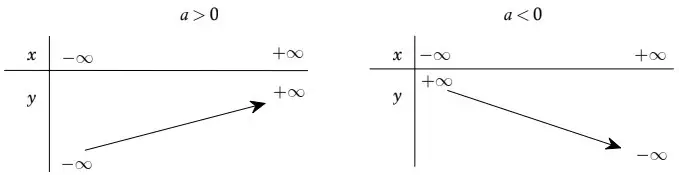 Bảng biến thiên[/caption]
Bảng biến thiên[/caption]

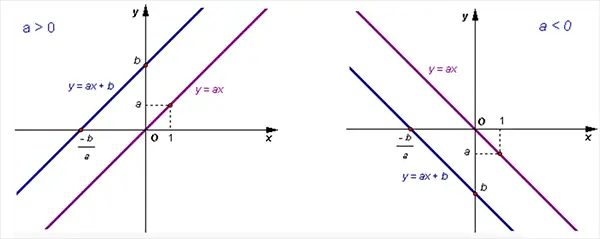
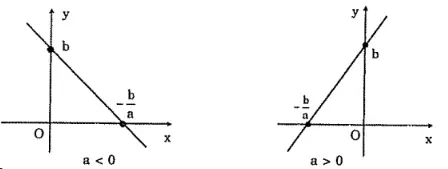 Trường hợp 2: Khi b khác 0
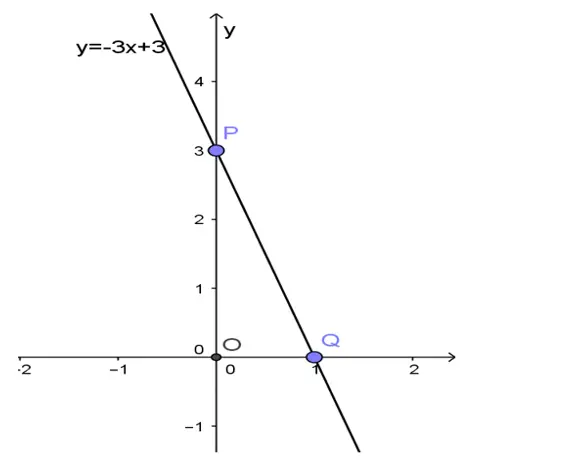
Trường hợp 2: Khi b khác 0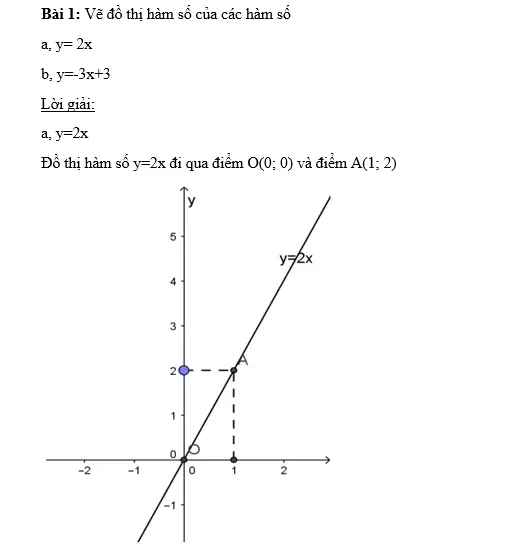






 Hình thang vuông[/caption]
Hình thang vuông[/caption]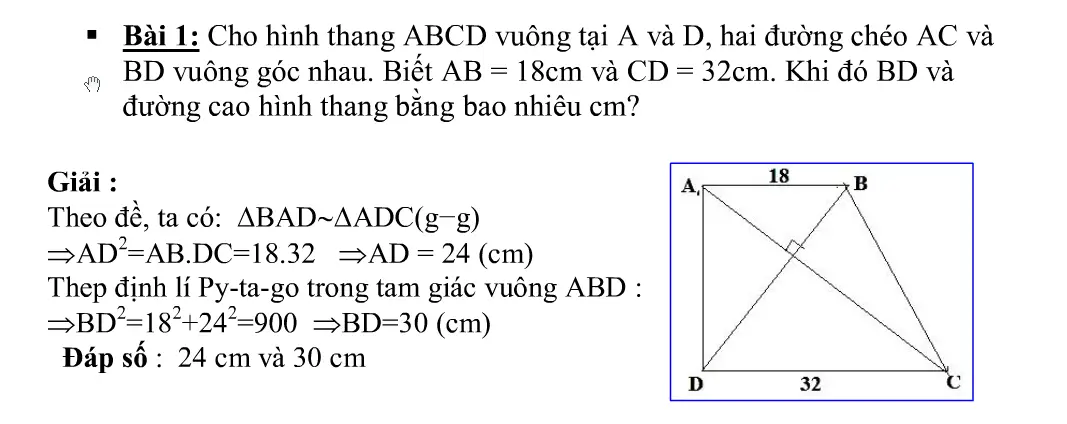 Bài tập về hình thang vuông[/caption]
Bài tập về hình thang vuông[/caption]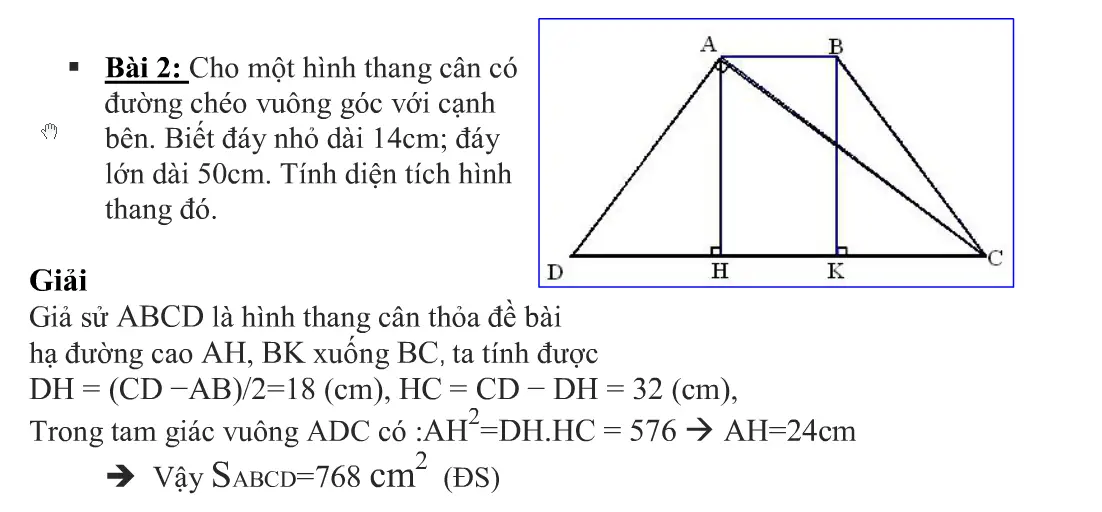 Bài tập về hình thang vuông[/caption]
Bài tập về hình thang vuông[/caption] Bài tập về hình thang vuông[/caption]
Bài tập về hình thang vuông[/caption]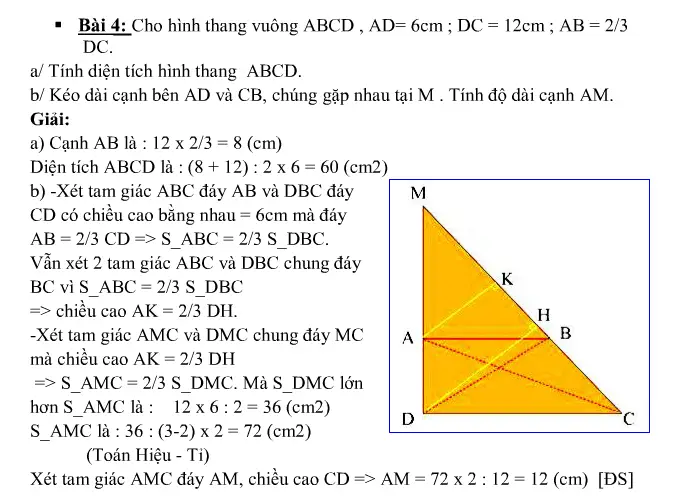 Bài tập về hình thang vuông[/caption]
Bài tập về hình thang vuông[/caption]